A consulting company tracks their consultant headcount with Hires, Terminations and Transfers. Their consultant “inventory” is derived into [Begin Count] and [End Count]. Nearly all other metrics rely upon the beginning and ending headcounts for such things as FTE utilization, average cost per FTE, etc. A consulting company really has no other capital assets making headcount very important.
The problem stems from the calculations where [End Count] relies on [Begin Count]. We’d like calculations which are easy to maintain and get good query performance for reports and ad-hoc quiries.
Implementation Platform:
Cube based calculated members in SQL Server Analysis Services 2005.
Business Definitions:
[End Count] = [Begin Count] + [Termination Count] + [Hire Count] + [Transfer Count]
[Begin Count] = [End Count] of the prior period. Example: [End Count] for Week 22 is 120 which becomes the [Begin Count] for Week 23.
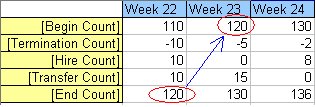
[Termination Count], [Hire Count], and [Transfer Count] are loaded measures.
Solution #1:
An elegant solution is available by taking advantage of the .PrevMember function in MDX.
We define [Begin Count] as:
MEMBER Measures.[Begin Count] AS
'
([Calendars].[Calendars].CurrentMember.PrevMember, Measures.[End Count])
'
From our example above Week 24 [Begin Count] is the [End Count] for Week 23 which is the value 130. Week 23 [Begin Count] is the [End Count] for Week 22 which is the value 120. If we had more data history the same pattern is followed.
We define [End Count] as:
MEMBER Measures.[End Count] AS
'
Measures.[Begin Count]
+ [Measures].[Hire Count]
+ [Measures].[Termination Count]
+ [Measures].[Transfer Count]'
Referencing [Begin Count] within the addition executed of [End Count] introduces a recursive definition where every [End Count] calculation uses [Begin Count] which in turn references [End Count].
For those familiar with recursive solutions (such as the Tower of Hanoi) you should recognize there is no “end point” to end the recursion. Recursive solutions typically have a check which tells the recursion to quit and return. As an example here is pseudo-code for a recursive function:
Function SolveIt( N, Src, Aux, Dst)
Begin
If N = 0 Then Exit Function
Else
Begin
SolveIt(N-1, Src, Dst, Aux)
Move from Src to Dest
SolveIt(N-1, Aux, Src, Dst)
End
End
The line “If N = 0 Then Exit Function” is our exit criteria for the recursion.
Our definition of [Begin Count] does not contain exit criteria for the recursion. Instead of an explicit exit criteria we rely upon an implied recursion end point from Analysis Services. The implied recursion end point comes from using:
[Calendars].[Calendars].CurrentMember.PrevMember
Eventually .PrevMember will reference a date outside the cube space. When the reference occurs the tuple ([Calendars].[Calendars].CurrentMember.PrevMember, Measures.[End Count]) returns NULL ending the recursion.
As an example we have a very limited calendar dimension with only 5 consecutive weeks. The data shown is for a division of the company which started in Week 20 by transferring 100 employees into the division and hiring 5 new employees.
The Week 20 [Begin Count] is null because it references .PrevMember which doesn’t exist. If we intercepted the [Begin Count] definition while Week 20 is the CurrentMember the tuple would look like this:
([Calendars].[Calendars].[Week 20].PrevMember, Measures.[End Count])
There is no previous member for Week 20 which results in a null value for the tuple form Analysis Services.
A problem arises with Solution #1 when we have a even a small number of members to recurse through which resolves [Begin Count]. Performance of [Begin Count] can get very slow. As an example a Calendar dimension with 12 years with a hierarchy of Year-Quarter-Month-Day has 4380 day level members (365 * 12). The above solution can take up to 30 minutes to return (on a 2 processor 2GB dev server) when getting Calendar.CurrentMember is a day member. We can improve performance by modifying the above calculated members. The modification is described below in Solution #2.
Solution #2:
This solution is an expansion of Solution #1 modified to take advantage of the non-additive nature of [Begin Count]. Solution #2 relies upon the [Begin Count] quality where [Begin Count] is the same value for the first member in a period regardless of which level the member belongs to in the Calendar hierarchy. For example, if [Begin Count] is 150 for the year 2006, the [Begin Count] is the same value (150) for Q1-2006, and the same for Jan-2006, and the same for 1 Jan 2006.
Calendar Member [Begin Count]
------------------ --------------
2006 150
Q1-2006 150
Jan 2006 150
1 Jan 2006 150
Solution #2 exploits the quality where the Parent of a member has the same [Begin Count] value as the member if the member is the first sibling of the parent.The following MDX is used in Solution#2.
MEMBER Measures.[New End Count] AS
'
IIF([Calendars].[Calendars].CurrentMember.Parent.Properties("KEY") = "3" // At the [Calendars].[Calendars].[Calendar Group].&[Fiscal] so go to first year.
, // TRUE
([Calendars].[Calendars].[Calendar Group].&[Fiscal].FirstChild ,[Measures].[Hire Count])
+ ([Calendars].[Calendars].[Calendar Group].&[Fiscal].FirstChild, [Measures].[Termination Count])
+ ([Calendars].[Calendars].[Calendar Group].&[Fiscal].FirstChild, [Measures].[Transfer Count])
, // FALSE
Measures.[New Begin Count]
+ [Measures].[Hire Count]
+ [Measures].[Termination Count]
+ [Measures].[Transfer Count]
)
'
[End Count] is an IIF() which is described in the following pseudo-code:
Function [End Count]
IF Calendar.CurrentMember.Parent is the highest valid point in the hierarchy THEN
Add up the Hire, Termination, and Transfer counts related to
the [Fiscal] member as [End Count].
This is the end point of our recursion.
ELSE
Add up Begin, Termination, Hire, and Transfer count as [End Count].
The reference to [Begin Count] force us to recurse back to the
[Begin Count] definition.
ENDIF
MEMBER Measures.[New Begin Count] AS
'
IIF([Calendars].[Calendars].CurrentMember.FirstSibling.Properties("ID") =
[Calendars].[Calendars].CurrentMember.Properties("ID")
, // TRUE
([Calendars].[Calendars].CurrentMember.Parent, Measures.[New Begin Count])
, // FALSE
([Calendars].[Calendars].CurrentMember.PrevMember, Measures.[New End Count])
)
'
The IIF() statement in [Begin Count] is best described with the following pseudo-code:
Function [Begin Count]
IF Calendar.CurrentMember is the first sibling THEN
Use [Begin Count] with Calendar.CurrentMember.Parent
ELSE
Use [End Count] with Calendar.CurrentMember.PrevMember
ENDIF
Using the technique where we look for the parents of first siblings allows the evaluation of [Begin Count] with far fewer recursive calls than if we use the recursive technique in Solution #1. The reduction in the number of recursive calls is what makes Solution #2 execute at an acceptable speed.


2 comments:
Hi Paul,
I googled and came across your post about begin and end counts. I was wondering if you could help me with adding an average to the measure group. I want to see, in your example, what the average number of employees was over the selected period.
A simple ([Start count] + [End count]) / 2 will not work because if we hire 10 people on monday and fire them on friday the avarag will not count these 10 people as we should do... Can you please give a hint on how to create this measure?
TIA.
Hi Ferdinand:
My apologies for the delayed reply, but I was not monitoring email over the weekend and yesterday was a holiday.
You ask:
>I was wondering if you could help me with adding an average to the measure group. I want to see, in your example, what the average number of employees was over the selected period.
>A simple ([Start count] + [End count]) / 2 will not work because if we hire 10 people on monday and fire them on friday the avarag will not count these 10 people as we should do... Can you please give a hint >on how to create this measure?
You are correct about the simpe (Start Count + End Count)/2 not providing the correct answer. The average calculation typically does a sum across the lowest level of the hierarchy and divides the sume by the number of elements included in the sum. The tricky part is determining the level in the hierarchy to use int he SUM(). Additionally with MDX we can use the AVG() function where the arguments are a set and a numeric expression:
Avg( Set_Expression [ , Numeric_Expression ] )
In your case I recommend using the AVG function, and ignore the sample in the BLOG outlining how to get that tricky StartCount and EndCount. The calculated member would look something like this which is a an example of a calculated member which works against the AdventureWorks cube:
WITH MEMBER Measures.[MyAvgSales] AS
'AVG({[Date].[Calendar].[Date].[January 10, 2003]:[Date].[Calendar].[Date].[January 20, 2003]}, [Measures].[Internet Sales Amount])'
SELECT{[Measures].[Internet Sales Amount], Measures.[MyAvgSales]} ON COLUMNS
,{[Date].[Calendar].[Date].[January 10, 2003]:[Date].[Calendar].[Date].[January 20, 2003]} ON ROWSFROM
[Adventure Works]
Hope this helps.
Best Regards,
PaulG
Post a Comment